If Ourcampus! Could Improve The Mean Time By Five Seconds, How Would The Probabilities Change?

Discrete Random Variables

24 Poisson Distribution

Another useful probability distribution is the Poisson distribution, or waiting fourth dimension distribution. This distribution is used to make up one's mind how many checkout clerks are needed to proceed the waiting time in line to specified levels, how may phone lines are needed to continue the system from overloading, and many other applied applications. A modification of the Poisson, the Pascal, invented nearly four centuries ago, is used today past telecommunication companies worldwide for load factors, satellite hookup levels and Internet capacity problems. The distribution gets its name from Simeon Poisson who presented information technology in 1837 as an extension of the binomial distribution which nosotros volition run across can be estimated with the Poisson.

At that place are two master characteristics of a Poisson experiment.

The Poisson probability distribution gives the probability of a number of events occurring in a fixed interval of time or space if these events happen with a known average rate.
The events are independently of the fourth dimension since the last event. For example, a book editor might exist interested in the number of words spelled incorrectly in a particular book. It might be that, on the boilerplate, there are v words spelled incorrectly in 100 pages. The interval is the 100 pages and it is causeless that in that location is no human relationship between when misspellings occur.
The random variable X = the number of occurrences in the interval of interest.

A depository financial institution expects to receive six bad checks per day, on average. What is the probability of the bank getting fewer than five bad checks on any given day? Of interest is the number of checks the banking company receives in one mean solar day, so the fourth dimension interval of interest is one solar day. Allow X = the number of bad checks the banking company receives in one day. If the bank expects to receive six bad checks per day then the average is 6 checks per day. Write a mathematical argument for the probability question.

P(x < 5)

You lot notice that a news reporter says "uh," on average, 2 times per broadcast. What is the probability that the news reporter says "uh" more two times per broadcast.

This is a Poisson trouble because you are interested in knowing the number of times the news reporter says "uh" during a broadcast.

a. What is the interval of interest?

a. one circulate measured in minutes

b. What is the boilerplate number of times the news reporter says "uh" during one broadcast?

c. Let X = ____________. What values does X take on?

c. Let X = the number of times the news reporter says "uh" during one broadcast.
x = 0, i, 2, 3, …

d. The probability question is P(______).

d. P(x > two)

Notation for the Poisson: P = Poisson Probability Distribution Function

X ~ P(μ)

Read this as "X is a random variable with a Poisson distribution." The parameter is μ (or λ); μ (or λ) = the mean for the interval of involvement. The mean is the number of occurrences that occur on average during the interval period.

The formula for computing probabilities that are from a Poisson process is:

$P\left(x\right)=\frac{{\mu }^{x}{e}^{-\mu }}{x!}$

where P(X) is the probability of X successes, μ is the expected number of successes based upon historical data, e is the natural logarithm approximately equal to 2.718, and X is the number of successes per unit, commonly per unit of time.

In order to use the Poisson distribution, certain assumptions must concord. These are: the probability of a success, μ, is unchanged within the interval, at that place cannot be simultaneous successes within the interval, and finally, that the probability of a success among intervals is independent, the aforementioned supposition of the binomial distribution.

In a fashion, the Poisson distribution can be thought of equally a clever fashion to convert a continuous random variable, usually fourth dimension, into a discrete random variable by breaking upwards time into detached independent intervals. This manner of thinking about the Poisson helps the states understand why it tin exist used to gauge the probability for the discrete random variable from the binomial distribution. The Poisson is asking for the probability of a number of successes during a menstruation of time while the binomial is request for the probability of a certain number of successes for a given number of trials.

Leah's answering car receives nigh six telephone calls betwixt 8 a.1000. and 10 a.thousand. What is the probability that Leah receives more than than i call in the next 15 minutes?

Let X = the number of calls Leah receives in 15 minutes. (The interval of interest is 15 minutes or $\frac{1}{4}$ hr.)

10 = 0, i, 2, 3, …

If Leah receives, on the average, half-dozen telephone calls in two hours, and there are eight 15 minute intervals in 2 hours, then Leah receives

$\left(\frac{1}{8}\right)$ (6) = 0.75 calls in 15 minutes, on average. And then, μ = 0.75 for this trouble.

10 ~ P(0.75)

Find P(10 > 1). P(x > 1) = 0.1734

Probability that Leah receives more than than one phone call in the next 15 minutes is most 0.1734.

The graph of Ten ~ P(0.75) is:

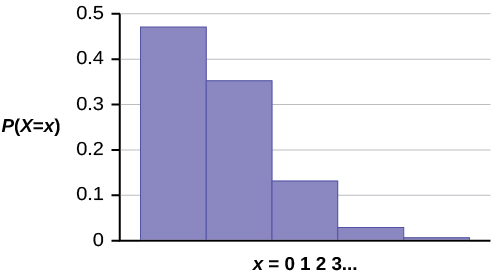
This graphs shows a poisson probability distribution. It has 5 bars that decrease in height from left to right. The x-axis shows values in increments of 1 starting with 0, representing the number of calls Leah receives within 15 minutes. The y-axis ranges from 0 to 0.5 in increments of 0.1.

The y-axis contains the probability of 10 where X = the number of calls in 15 minutes.

Co-ordinate to a survey a academy professor gets, on average, 7 emails per day. Let X = the number of emails a professor receives per day. The detached random variable X takes on the values x = 0, 1, 2 …. The random variable 10 has a Poisson distribution: X ~ P(7). The mean is seven emails.

What is the probability that an email user receives exactly 2 emails per day?
What is the probability that an email user receives at most two emails per 24-hour interval?
What is the standard difference?

Text message users receive or send an average of 41.v text letters per 24-hour interval.

How many text letters does a text message user receive or send per hour?
What is the probability that a text bulletin user receives or sends ii messages per 60 minutes?
What is the probability that a text message user receives or sends more than than ii messages per 60 minutes?

On May 13, 2013, starting at 4:thirty PM, the probability of low seismic activity for the next 48 hours in Alaska was reported equally well-nigh 1.02%. Use this data for the next 200 days to find the probability that there will be low seismic activity in ten of the next 200 days. Use both the binomial and Poisson distributions to calculate the probabilities. Are they shut?

Let X = the number of days with depression seismic activity.

Using the binomial distribution:

$P\left(x=10\right)=\frac{200!}{10!\left(200-10\right)!}×{.0102}^{10}=0.000039$

Using the Poisson distribution:

Calculate μ = np = 200(0.0102) ≈ 2.04
$P\left(x=10\right)=\frac{{\mu }^{x}{e}^{\mathrm{-\mu }}}{\mathrm{x!}}=\frac{{2.04}^{10}{e}^{-2.04}}{10!}=0.000045$

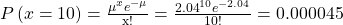
Nosotros wait the approximation to be practiced considering n is large (greater than 20) and p is small (less than 0.05). The results are close—both probabilities reported are well-nigh 0.

Estimating the Binomial Distribution with the Poisson Distribution

Nosotros found before that the binomial distribution provided an approximation for the hypergeometric distribution. At present we find that the Poisson distribution tin provide an approximation for the binomial. Nosotros say that the binomial distribution approaches the Poisson. The binomial distribution approaches the Poisson distribution is equally due north gets larger and p is small-scale such that np becomes a constant value. There are several rules of thumb for when one can say they will use a Poisson to estimate a binomial. One suggests that np, the mean of the binomial, should be less than 25. Another author suggests that information technology should be less than 7. And some other, noting that the mean and variance of the Poisson are both the aforementioned, suggests that np and npq, the mean and variance of the binomial, should be greater than 5. There is no one broadly accepted rule of thumb for when one can use the Poisson to judge the binomial.

Every bit nosotros move through these probability distributions we are getting to more sophisticated distributions that, in a sense, contain the less sophisticated distributions within them. This proposition has been proven by mathematicians. This gets us to the highest level of composure in the next probability distribution which can be used as an approximation to all of those that we have discussed then far. This is the normal distribution.

A survey of 500 seniors in the Toll Concern Schoolhouse yields the post-obit information. 75% become straight to work after graduation. 15% go on to piece of work on their MBA. nine% stay to go a small in some other program. 1% continue to go a Main'southward in Finance.

What is the probability that more than 2 seniors go to graduate school for their Chief'due south in finance?

This is clearly a binomial probability distribution problem. The choices are binary when we define the results as "Graduate School in Finance" versus "all other options." The random variable is discrete, and the events are, nosotros could assume, independent. Solving equally a binomial problem, we have:

Binomial Solution

$n·p=500·0.01=5=µ$

$P\left(0\right)=\frac{500!}{0!\left(500-0\right)!}{0.01}^{0}\left(1-0.01{\right)}^{{500}^{{-}^{0}}}=0.00657$

$P\left(1\right)=\frac{500!}{1!\left(500-1\right)!}{0.01}^{1}\left(1-0.01{\right)}^{{500}^{{-}^{1}}}=0.03318$

$P\left(2\right)=\frac{500!}{2!\left(500-2\right)!}{0.01}^{2}\left(1-0.01{\right)}^{{500}^{{-}^{2}}}=0.08363$

Adding all 3 together = 0.12339

$1-0.12339=0.87661$

Poisson approximation

$n·p=500·0.01=5=\mu$

$n·p·\left(1-p\right)=500·0.01·\left(0.99\right)\approx 5={\sigma }^{2}=\mu$

$P\left(X\right)=\frac{{e}^{{\mathrm{-np}}^{}}\left(np{\right)}^{x}}{x!}=\left\{P\left(0\right)=\frac{{e}^{-5}·{5}^{0}}{0!}\right\}+\left\{P\left(1\right)=\frac{{e}^{-5}·{5}^{1}}{1!}\right\}+\left\{P\left(2\right)=\frac{{e}^{-5}·{5}^{2}}{2!}\right\}$

$0.0067+0.0337+0.0842=0.1247$

$1-0.1247=0.8753$

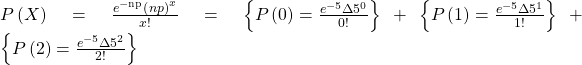
An approximation that is off past one ane thousandth is certainly an adequate approximation.

Affiliate Review

A Poisson probability distribution of a discrete random variable gives the probability of a number of events occurring in a stock-still interval of time or space, if these events happen at a known average rate and independently of the time since the concluding outcome. The Poisson distribution may exist used to approximate the binomial, if the probability of success is "small" (less than or equal to 0.01) and the number of trials is "big" (greater than or equal to 25). Other rules of thumb are also suggested by different authors, just all recognize that the Poisson distribution is the limiting distribution of the binomial as due north increases and p approaches zero.

The formula for computing probabilities that are from a Poisson process is:

$P\left(x\right)=\frac{{\mu }^{x}{e}^{-\mu }}{x!}$

where P(X) is the probability of successes, μ (pronounced mu) is the expected number of successes, due east is the natural logarithm approximately equal to 2.718, and Ten is the number of successes per unit, commonly per unit of time.

Formula Review

X ~ P(μ) ways that X has a Poisson probability distribution where X = the number of occurrences in the interval of interest.

X takes on the values x = 0, ane, ii, 3, …

The mean μ or λ is typically given.

The variance is σ ⁱⁱ = μ, and the standard deviation is
$\sigma \text{ = }\sqrt{\mu }$ .

When P(μ) is used to gauge a binomial distribution, μ = np where due north represents the number of independent trials and p represents the probability of success in a single trial.

$P\left(x\right)=\frac{{\mu }^{x}{e}^{-\mu }}{x!}$

Use the following information to answer the next six exercises: On boilerplate, a clothing store gets 120 customers per day.

Assume the effect occurs independently in any given twenty-four hours. Define the random variable X.

<!– <solution id="fs-idm218580928″> X ~ P(120) –>

What values does X have on?

0, i, ii, iii, 4, …

What is the probability of getting 150 customers in one day?

<!– <solution id="fs-idm98751248″> 0.0010 –>

What is the probability of getting 35 customers in the outset four hours? Assume the store is open 12 hours each day.

0.0485

What is the probability that the store will take more than 12 customers in the offset hr?

<!– <solution id="fs-idm122562880″> 0.2084 –>

What is the probability that the store will have fewer than 12 customers in the first two hours?

0.0214

Which type of distribution can the Poisson model be used to approximate? When would y'all exercise this?

<!– <solution id="fs-idm58434144″> The Poisson distribution can approximate a binomial distribution, which you would do if the probability of success is modest and the number of trials is big. –>

Use the post-obit information to reply the next half-dozen exercises: On boilerplate, viii teens in the U.Southward. die from motor vehicle injuries per solar day. As a issue, states across the country are debating raising the driving age.

Assume the upshot occurs independently in any given mean solar day. In words, define the random variable X.

Ten = the number of U.S. teens who die from motor vehicle injuries per day.

X ~ _____(_____,_____)

<!– <solution id="fs-idp14476864″> P(8) –>

What values does X take on?

0, 1, 2, iii, 4, …

For the given values of the random variable X, fill in the corresponding probabilities.

<!– <solution id="fs-idp29073952″>

–>

Is it probable that there volition be no teens killed from motor vehicle injuries on any given 24-hour interval in the U.Southward? Justify your answer numerically.

Is it likely that there will be more than xx teens killed from motor vehicle injuries on any given day in the U.S.? Justify your respond numerically.

<!– <solution id="id10039877″> No –>

HOMEWORK

The switchboard in a Minneapolis police office gets an average of 5.5 incoming telephone calls during the noon 60 minutes on Mondays. Experience shows that the existing staff can handle up to half dozen calls in an 60 minutes. Let 10 = the number of calls received at noon.

Find the mean and standard deviation of 10.
What is the probability that the office receives at most 6 calls at noon on Mon?
Find the probability that the law office receives half dozen calls at noon. What does this hateful to the law office staff who get, on average, 5.five incoming phone calls at noon?
What is the probability that the office receives more than eight calls at noon?

X ~ P(5.5); μ = 5.5; 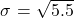$\sigma \text{ = }\sqrt{5.5}$ ≈ ii.3452
P(10 ≤ vi) ≈ 0.6860
There is a 15.7% probability that the law staff volition receive more calls than they can handle.
P(x > 8) = i – P(x ≤ eight) ≈ 1 – 0.8944 = 0.1056

The maternity ward at Dr. Jose Fabella Memorial Hospital in Manila in the Philippines is one of the busiest in the world with an average of 60 births per day. Allow X = the number of births in an hour.

Find the mean and standard deviation of Ten.
Sketch a graph of the probability distribution of X.
What is the probability that the motherhood ward will evangelize iii babies in one hour?
What is the probability that the maternity ward will deliver at most three babies in one hour?
What is the probability that the maternity ward volition deliver more v babies in ane hour?

<!– <solution id="fs-idm62476208″> X ~ P(2.5); μ = two.5; σ = 2.five ≈ i.5811

P(x = 3) = poissonpdf(2.five, three) ≈ 0.2138 P(x ≤ three) = poissoncdf(2.v, 3) ≈ 0.7576 P(x > 5) = one – P(x ≤ v) = 1 – poissoncdf(two.5, 5) ≈ 0.0420 –>

A manufacturer of Christmas tree calorie-free bulbs knows that 3% of its bulbs are lacking. Notice the probability that a cord of 100 lights contains at well-nigh four defective bulbs using both the binomial and Poisson distributions.

Let X = the number of defective bulbs in a cord.

Using the Poisson distribution:

μ = np = 100(0.03) = 3
Ten ~ P(3)
P(x ≤ 4) ≈ 0.8153

Using the binomial distribution:

X ~ B(100, 0.03)
P(10 ≤ 4) = 0.8179

The Poisson approximation is very proficient—the difference betwixt the probabilities is only 0.0026.

The average number of children a Japanese woman has in her lifetime is one.37. Suppose that one Japanese woman is randomly chosen.

In words, define the random variable X.
Listing the values that X may take on.
Find the probability that she has no children.
Find the probability that she has fewer children than the Japanese average.
Find the probability that she has more children than the Japanese average.

The average number of children a Spanish woman has in her lifetime is 1.47. Suppose that 1 Spanish adult female is randomly chosen.

In words, define the Random Variable 10.
List the values that X may take on.
Find the probability that she has no children.
Find the probability that she has fewer children than the Castilian average.
Find the probability that she has more children than the Spanish average .

X = the number of children for a Spanish woman
0, 1, 2, three,…
0.2299
0.5679
0.4321

Fertile, female cats produce an average of three litters per twelvemonth. Suppose that 1 fertile, female person cat is randomly called. In one twelvemonth, find the probability she produces:

In words, ascertain the random variable 10.
List the values that X may take on.
Give the distribution of X. X ~ _______
Observe the probability that she has no litters in ane twelvemonth.
Discover the probability that she has at least two litters in one twelvemonth.
Notice the probability that she has exactly three litters in one year.

<!– <solution id="fs-idp96709152″> X = the number of litters a fertile, female true cat produces per year 0, i, 2, iii, … 10 ~ P(3) 0.0498 0.8009 0.2240 –>

The chance of having an extra fortune in a fortune cookie is about 3%. Given a pocketbook of 144 fortune cookies, we are interested in the number of cookies with an extra fortune. Two distributions may be used to solve this problem, but only use ane distribution to solve the problem.

In words, define the random variable X.
List the values that Ten may accept on.
How many cookies do nosotros expect to take an extra fortune?
Detect the probability that none of the cookies have an actress fortune.
Find the probability that more than iii have an extra fortune.
Every bit due north increases, what happens involving the probabilities using the 2 distributions? Explicate in consummate sentences.

X = the number of fortune cookies that accept an extra fortune
0, 1, 2, 3,… 144
iv.32
0.0124 or 0.0133
0.6300 or 0.6264
As north gets larger, the probabilities go closer together.

According to the South Carolina Department of Mental Health web site, for every 200 U.S. women, the boilerplate number who endure from anorexia is one. Out of a randomly called group of 600 U.South. women make up one's mind the post-obit.

In words, ascertain the random variable X.
List the values that 10 may have on.
Give the distribution ofX. Ten ~ _____(_____,_____)
How many are expected to suffer from anorexia?
Find the probability that no ane suffers from anorexia.
Find the probability that more four suffer from anorexia.

<!– <solution id="id13728739″> X = the number of women that suffer from anorexia 0, 1, 2, 3, …, 600 X ~ P(3) 3 0.0498 0.1847 –>

The risk of an IRS inspect for a tax render with over ?25,000 in income is about 2% per year. Suppose that 100 people with tax returns over ?25,000 are randomly picked. We are interested in the number of people audited in 1 twelvemonth. Use a Poisson distribution to anwer the following questions.

In words, define the random variable Ten.
Listing the values that 10 may take on.
How many are expected to be audited?
Find the probability that no one was audited.
Observe the probability that at least three were audited.

X = the number of people audited in one yr
0, 1, 2, …, 100
2
0.1353
0.3233

Approximately 8% of students at a local high school participate in after-school sports all 4 years of high school. A grouping of 60 seniors is randomly chosen. Of involvement is the number that participated in after-school sports all four years of high school.

In words, define the random variable X.
List the values that 10 may take on.
How many seniors are expected to have participated in after-school sports all four years of high school?
Based on numerical values, would you be surprised if none of the seniors participated in after-schoolhouse sports all 4 years of loftier school? Justify your answer numerically.
Based on numerical values, is information technology more likely that four or that five of the seniors participated in after-school sports all four years of high school? Justify your answer numerically.

<!– <solution id="id18997392″> X = the number of seniors who participated in after-school sports all four years of high school 0, i, 2, 3, … sixty 4.8 Yes 4 –>

On boilerplate, Pierre, an apprentice chef, drops three pieces of egg beat into every two cake batters he makes. Suppose that you buy one of his cakes.

In words, define the random variable Ten.
List the values that X may take on.
On boilerplate, how many pieces of egg shell do you wait to be in the cake?
What is the probability that in that location will not be any pieces of egg shell in the cake?
Allow'due south say that y'all buy ane of Pierre's cakes each calendar week for 6 weeks. What is the probability that there will non exist whatsoever egg shell in any of the cakes?
Based upon the boilerplate given for Pierre, is information technology possible for there to be vii pieces of beat in the cake? Why?

10 = the number of crush pieces in one block
0, 1, 2, iii,…
i.v
0.2231
0.0001
Yes

Use the post-obit data to reply the next two exercises: The average number of times per week that Mrs. Plum'south cats wake her up at night considering they desire to play is ten. We are interested in the number of times her cats wake her up each week.

In words, the random variable X = _________________

the number of times Mrs. Plum'south cats wake her up each week.
the number of times Mrs. Plum'due south cats wake her up each hour.
the number of times Mrs. Plum's cats wake her up each night.
the number of times Mrs. Plum's cats wake her up.

<!– <solution id="id13453446″> a –>

Find the probability that her cats will wake her up no more than five times side by side week.

0.5000
0.9329
0.0378
0.0671

Primal Terms

Poisson Probability Distribution

a discrete random variable (RV) that counts the number of times a certain event will occur in a specific interval; characteristics of the variable:

The probability that the event occurs in a given interval is the same for all intervals.
The events occur with a known mean and independently of the time since the last event.

The distribution is divers past the mean μ of the event in the interval. The mean is μ = np. The standard deviation is 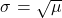$\sigma \text{ = }\sqrt{\mu }$ . The probability of having exactly 10 successes in r trials is 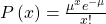$P\left(x\right)=\frac{{\mu }^{x}{e}^{-\mu }}{x!}$ . The Poisson distribution is often used to approximate the binomial distribution, when n is "large" and p is "minor" (a general rule is that np should be greater than or equal to 25 and p should exist less than or equal to 0.01).

Source: https://opentextbc.ca/introbusinessstatopenstax/chapter/poisson-distribution/

Posted by: malaveplairt.blogspot.com

If Ourcampus! Could Improve The Mean Time By Five Seconds, How Would The Probabilities Change?

24 Poisson Distribution

Notation for the Poisson: P = Poisson Probability Distribution Function

Estimating the Binomial Distribution with the Poisson Distribution

Affiliate Review

Formula Review

HOMEWORK

Primal Terms

0 Response to "If Ourcampus! Could Improve The Mean Time By Five Seconds, How Would The Probabilities Change?"

Post a Comment

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel